연세대 선형대수학 족보 2학기-선대시험-2차중간-모범답안

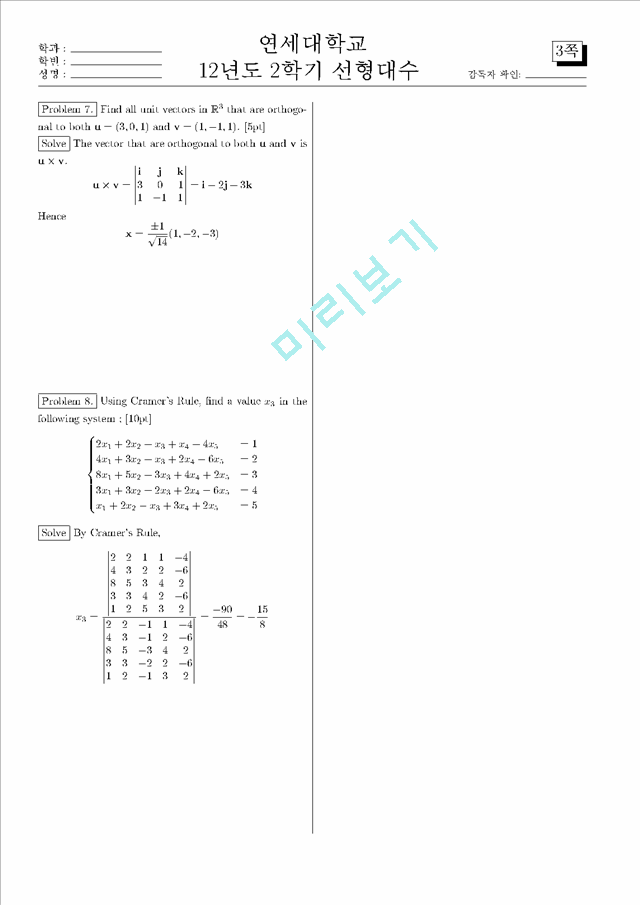
Problem 1. Indicate whether the statement is true(T) or (5) If A is an n×n matrix, and if the linear system Ax = b is consistent for every vector b in Rn , then TA : Rn → false(F). Justify your answer. [each 3pt] (1) If T1 : R → R (F)
2 3 n m

and T2 : R

m

→ R are linear trans-

k

formations, and if T1 is not onto, then neither is T2 T1 . Problem 3. Determine whether the linear transformation Solve Take T1 : R → R given by T1 (x, y) = (x, y, 0) is one-to-one and/or onto. Justify your answer. [each 5pt] and T2 : R3 → R2 given by T2 (x, y, z) = (x, y). Then (1) T : R3 → R3 , given by T (x, y, z) = (4x, 2x + y, x T is not onto, but T T is onto.
1 2 1

3y). (2) If the characteristic polynomial of A is p(λ) = λ λn1 + λ, then A is a singular matrix. (T) Solve Since det(A) = (1)n p(0) = 0, A is a singular matrix. (3) If A is orthogonal, then (det(A))2 = 1. (T) Solve Since A1 = AT and det(A) = det(AT), 1 = det(AA1) = det(A) det(A1) = (det(A))2 . (4) The determi…(생략)